Mere disperzije (varijabiliteta, varijacije, raspršenosti) pokazuju u kojoj meri su podaci više koncentrisani odnosno više raspršeni. Može se desiti da dve serije imaju istu aritmetičku sredinu, a da se pritom podaci u jednoj seriji grupisani jedan do drugog, dok su u drugoj značajno raspršeni.
Mere disperzije su numerički pokazatelji koji opisuju u kom se stepenu vrednosti u posmatranoj pojavi međusobno razlikuju.
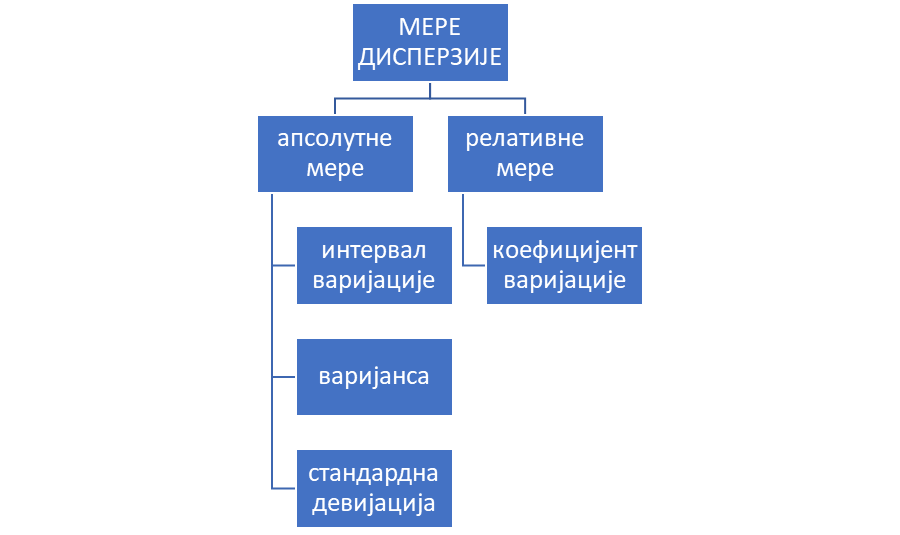
Prema jedinici mere u kojoj se izražavaju, mere disperzije se mogu podeliti u dve grupe:
- apsolutne mere disperzije, koje su izražene u istim jedinicama mere (kg,m,kom..) i
- relativne mere disperzije, koje su izražene u procentima ili nekim drugim jedinicama.
APSOLUTNE MERE DISPERZIJE
Interval varijacije (i)
Interval varijacije je najjednostavnija apsolutna mera disperzije, i koja predstavlja razliku između najvećeg i najmanjeg podatka.
Interval varijacije je aposolutna mera disperzije koja se dobija kao razlika između najveće i najmanje vrednosti posmatranog obeležja.
i=x_{\max}-\ x\ _{\min\ \left(1.1\right)}Najznačajniji nedostaci intervala varijacije jesu:
- što ova veličina zavisi od samo dva člana serije,
- na navednu meru ne utiče veličina serija i
- vrlo retko se koristi u praksi.
Varijansa (σ2 )
Varijansa (σ2 ) je aposolutna mera varijabiliteta koja predstavlja prosečno kvadratno odstupanje podataka u seriji od aritmetičke sredine te serije.
Vrijansa (σ2 )- čita se: sigma na kvadrat. Njena vrednost se kreće od nule do beskonačno.
Varijansa kod negrupisanih podataka
\sigma^2\ =\ \frac{(x_1-µ)^2+(x_2-µ)^2+(x_3-µ)^2}{n}+\frac{(x_4-µ)^2+(x_5-µ)^2+...+(x_n-µ)^2}{n}\ \left(1.2\right)\sigma^2\ =\ \frac{\sum_{i=1}^n(x_i-µ)^2}{n}\ \left(1.3\right)Varijansa kod grupisanih podataka – prekidno numeričko obeležje
\sigma^2\ =\ \frac{\sum_{i=1}^n\ f_i(x_i-µ)^2}{\sum_{i=1}^nf_i}\left(1.4\right)\sigma^2\ =\ \frac{\sum_{i=1}^n\ f_{i\ }\cdot\ x^2}{\sum_{i=1}^nf_i}-µ^2\ \left(1.5\right)Varijansa kod intervalno grupisanih podataka
\sigma^2\ =\ \frac{\sum_{i=1}^n\ f_{i\ }\left(\overline{X\ }-µ\right)^2}{\sum_{i=1}^nf_i}\ \left(1.6\right)\sigma^2\ =\ \frac{\sum_{i=1}^n\ f_{i\ }\cdot\ \overline{X\ }^2}{\sum_{i=1}^nf_i}-µ^2\ \left(1.7\right)Standardna devijacija (σ)
Najznačajniji problem kod interpretacije varijanse jeste to što se dobijaju velike vrednosti izražene u kvadratima obeležja. Zbog toga češće koristimo pokazatelj koji se naziva standardna devijacija. Standardna devijacija predstavlja kvadratni koren iz varijanse.
Standarda devijacija je aposolutna mera varijabiliteta koja pokazuje koliku u proseku odstupaju pojedinačne vrednosti od aritmetičke sredine.
σ=\sqrt{\sigma^2\ }Izračunavanje standardne devijacije kod negrupisanih podataka
σ=\sqrt{\sigma^2\ }=\ \sqrt{\frac{\sum_{i=1}^n\ (x_i-µ)^2}{\sum_{i=1}^nf_i}}\left(1.8\right)σ=\sqrt{\sigma^2\ }=\ \sqrt{\frac{\sum_{i=1}^n\ x_i^2}{\sum_{i=1}^nf_i}-µ^2}\left(1.9\right)Izračunavanje standardne devijacije kod grupisanih podataka
σ=\sqrt{\sigma^2\ }=\sqrt{\frac{\sum_{i=1}^n\ f_i(x_i-µ)^2}{\sum_{i=1}^nf_i}}\left(1.10\right)σ=\sqrt{\sigma^2\ }=\sqrt{\frac{\sum_{i=1}^n\ f_i\cdot x_i^{^2}}{\sum_{i=1}^nf_i}-µ^2}\ \left(1.11\right)Kod svih navedenih formula imenilac predstavlja broj članova serije, pa da li ćemo ga označavati na navedeni način ili kao N biće svejedno.
RELATIVNE MERE DISPERZIJE
Postoji više relativnih pokazatelja relativnih mera disperzije, ali ćemo ovde obraditi samo koeficijent varijacije.
Koeficijent varijacije je relativna mera varijabiliteta koja predstavlja odnos između standardne devijacije i aritmetičke sredine, iskazan u procentima.
Koeficijent (Kv) varijacije računa se po obrascu:
K_v=\ \frac{\sigma}{µ}\cdot100\ \left(1.12\right)Koeficijent varijacije pokazuje koliko procenata iznosi standardna devijacija u odnosu na aritmetičku sredinu.
